Giới thiệu về khái niệm “đồng thuận” trong hệ thống phân tán, các khó khăn và kết quả đã đạt được.

Paper https://raft.github.io/raft.pdf

Phần I: Đồng thuận trong hệ thống phân tán

Giới thiệu

Bài toán 2 đại tướng:

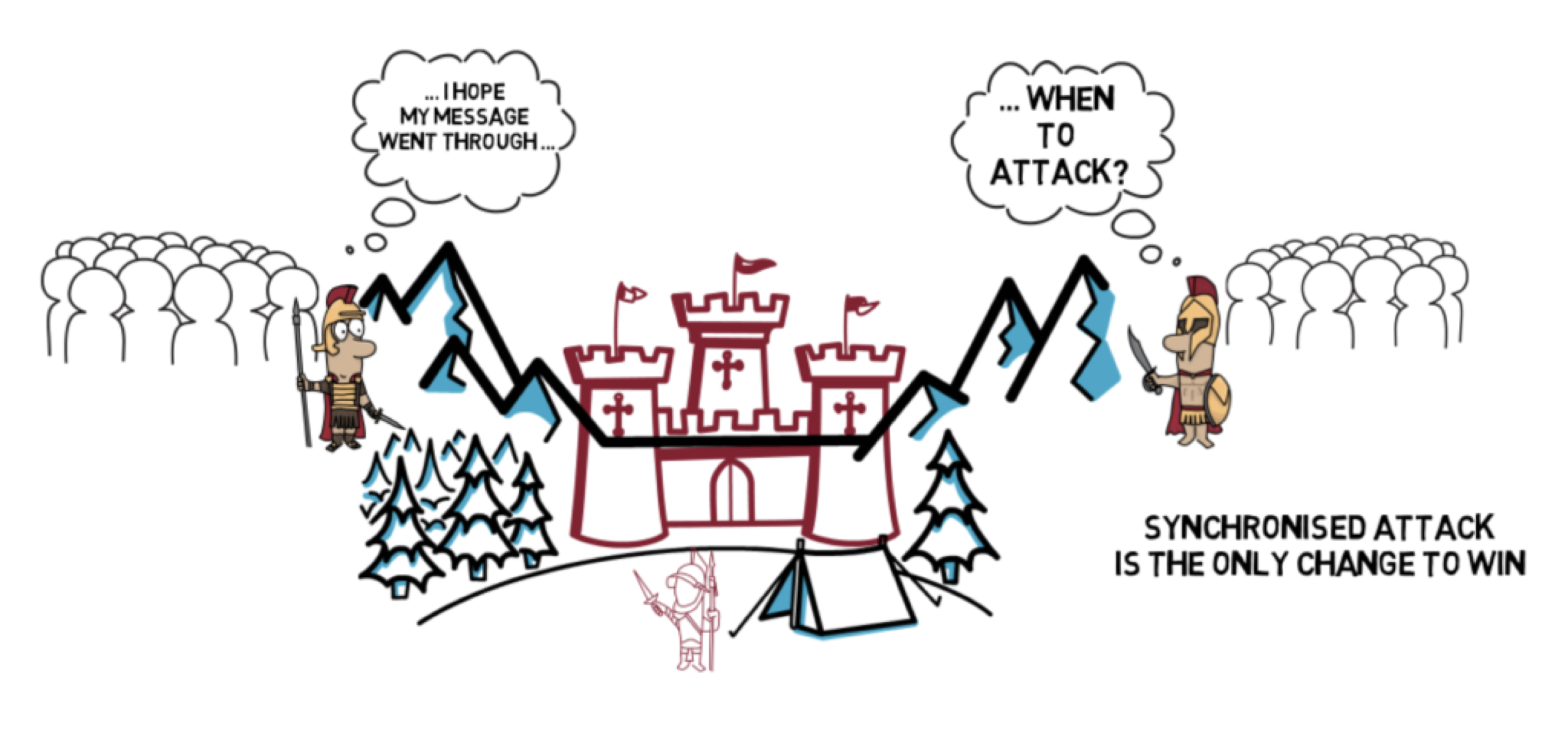
Có 2 vị tướng cầm các cánh quân khác nhau xung quanh thành phố mà họ dự định tấn công. Hai vị tướng chỉ có thể liên lạc thông qua lính truyền tin. Hai vị tướng cần phải thống nhất với nhau về quyết định tấn công hoặc rút lui. Do đó cần đồng thuận về một quyết định để cùng phối hợp với nhau.

Đội quân 1	Đội quân 2	Kết quả
Không đánh	Không đánh	Không có chuyện gì xảy ra
Không đánh	Đánh	Đội quân 2 bị thất bại
Đánh	Không đánh	Đội quân 1 bị thất bại
Đánh	Đánh	Đánh chiếm được thành phố

Từ bảng trên, nhận thấy kết quả tốt nhất ta muốn đạt được là cả 2 đội quân phải có chung quyết định đánh vào cùng một thời điểm. Và kết quả tệ nhất buộc phải tránh là hai vị tướng đưa ra hai quyết định khác nhau, dẫn đến kết quả bị thua.

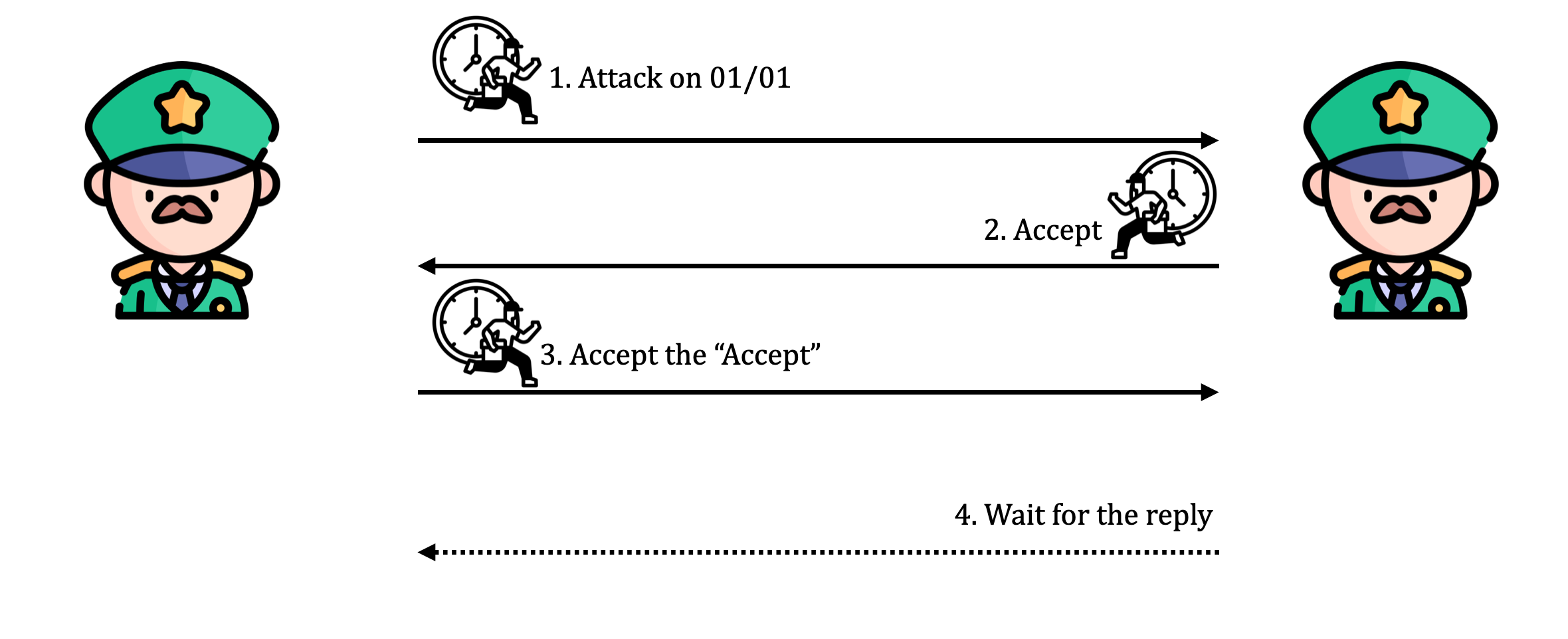
Ta có một kịch bản truyền tin như sau:

• Vị tướng A đưa phong thư cho giao liên gửi cho vị tướng B thống nhất giờ đánh.
• Vị tướng B nhận được, viết vào phong thư là đồng ý và giao liên sẽ gửi lại cho vị tướng A.
• Vị tướng A khi nhận được, có thể sẵn sàng ra trận. Tuy nhiên, vị tướng B vẫn không thể chắc chắn, vì có thể giao liên bị bắt nên vị tướng A không nhận được. Do vậy, vị tướng B tiếp tục chờ vị tướng A trả lời lại thông điệp đồng ý của mình.

Cứ thế, cả 2 vị tướng sẽ không bao giờ đạt được đồng thuận.

Minh hoạ cho 2 vị tướng liên tục chờ xác nhận thời gian trận đánh

Byzantine Generals’ Problem

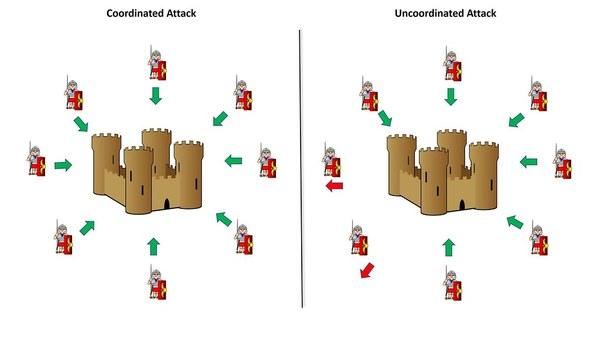Nếu ta thay đổi lại yêu cầu bài toán: từ 2 vị tướng thành N vị tướng. Tin tức lúc này có thể bị thất lạc hoặc giả mạo. Ngoài ra, trong trường hợp có những vị tướng phản bội ngăn cản các vị tướng làm theo thỏa thuận bằng cách gửi đi những thông điệp gây nhiễu. Ví dụ:

• 4 tướng muốn tấn công
• 4 tướng muốn rút quân
• Tướng phản bội nói với nhóm thứ nhất là muốn tấn công, nói với nhóm thứ 2 là muốn rút quân

Vậy các tướng trung thành làm thế nào để có thể đạt được thỏa thuận?

Tại sao đồng thuận trong hệ thống phân tán quan trọng

Ngữ cảnh trên tương tự như trong hệ thống phân tán: các máy tính trong mạng là các vị tướng; người đưa thư là phương tiện truyền tải thông tin; bức thư là thông tin mà các máy tính trong mạng muốn truyền tải.

• 2 generals problem: tương ứng với trường hợp khi hệ thống truyền tin gặp lỗi (link failure problem)
• Byzantine generals problem: tương ứng với trường hợp khi các node gặp lỗi (node failure problem)

Minh hoạ tương ứng giữa bài toán 2 vị trướng và giao tiếp giữa các máy trong mạng

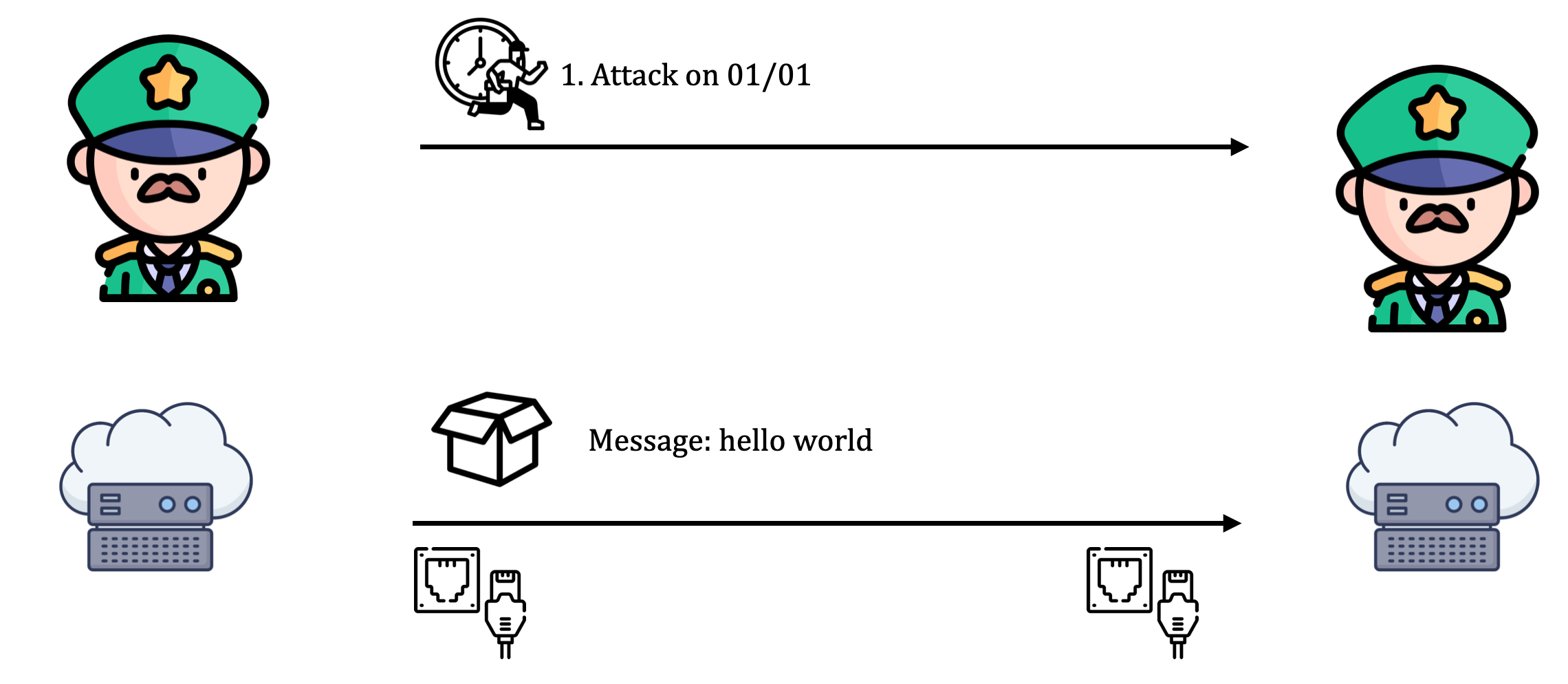
Từ hai ví dụ. trên, ta thấy việc gửi nhận thông tin trong hệ thống phân tán là rất khó vì tin nhắn có thể :

• Thất lạc trên đường truyền, không tới được người nhận.
• Nhận trễ với thời gian bất kì (nhận được sau 2 giây hoặc có thể sau một tiếng)
• Nhận được không đúng với thứ tự được gửi.
• Có thể bị gửi sai (byzantine) hoặc bị thay đổi nội dung trên đường truyền.
• …

Tuy vậy, yêu cầu đặt ra là các máy tính trong mạng cần phải đạt được đồng thuận trên cùng một thông tin, với khả năng chịu lỗi (fault-tolerance) hoặc ở máy tính hay ở trên mạng truyền tin. Đồng thuận là bài toán kinh điển luôn xuất hiện trong các hệ thống phân tán do có nhiều tác nhân tham gia.

Ví dụ thực tế với hệ thống Kafka, các brokers cần phải thống nhất thông tin về controller (là broker đóng vai trò là leader trên một topic). Tại một thời điểm, nếu có nhiều hơn 2 máy cùng là controller trên một topic có thể xảy ra tình trạng dữ liệu không nhất quán.

Các hệ thống phân tán luôn có service đảm bảo đồng thuận cho toàn bộ mạng, và được coi là trái tim của toàn bộ hệ thống. Ví dụ như Kafka sử dụng Zookeeper (sử dụng biến thể của thuật toán Paxos) hay Kubernetes sử dụng etcd (thuật toán Raft).

Các kết quả quan trọng trong hệ thống phân tán

Ta có thể chứng minh được rằng bài toán “Hai vị tướng” không thể tồn tại một thuật toán đồng thuận để 2 vị tướng có thể an toàn giao tiếp với điều kiện đề bài nêu trên.

Cụ thể hơn một thuật toán đồng thuận phải thỏa mãn 4 tính chất:

• Tính chấm dứt (Termination): các tiến trình hoạt động đúng sẽ dần đưa ra giá trị quyết định.
• Tính toàn vẹn (Integrity): các tiến trình hoạt động đúng chỉ quyết định một giá trị. Và nếu một tiến trình quyết định một giá trị v, giá trị v phải được đề xuất bởi một tiến trình đúng khác.
• Tính hiệu lực (Validity): nếu tất cả các tiến trình đề xuất giá trị v, mọi tiến trình chạy đúng phải chấp nhận giá trị v
• Thỏa thuận (Agreement): nếu một tiến trình chạy đúng chọn giá trị v, thì mọi tiến trình chạy đúng khác cũng phải chọn giá trị v

Hơn thế, một định lí quan trọng hơn trong hệ thống phân tán được gọi là FLP-Impossbility

Trong hệ thống mạng bất đồng bộ, khi mà các tin nhắn có thể nhận trễ vô thời hạn nhưng không bao giờ thất lạc, sẽ không tồn tại một thuật toán đồng thuận nào đảm bảo kết thúc trong mọi khả năng có thể thực thi, với mọi cấu hình ban đầu, khi tồn tại ít nhất một máy tính bị lỗi-và-dừng-hẳn.

Tác giả: Michael [F]ischer, Nancy [L]ynch and Michael [P]aterson - 1985

Ta phân tích định lí trên sẽ thấy các giả thiết được nêu ra là:

• Mô hình mạng: dựa trên mạng bất đồng bộ - không có giả thiết nào về thời gian hoặc thứ tự của các sự kiện mà máy tính trong mạng sẽ nhận được. Không có một đồng hồ chung các tiến trình cùng đồng ý, đồng thời đồng hồ trên mỗi máy tính có thể chạy khác nhau.
• Mô hình chịu lỗi (Failure model): có rất nhiều mô hình chịu lỗi trong hệ thống phân tán, tuy nhiên ta chỉ quan tâm đến mô hình lỗi-và-dừng-hẳn (fail-stop model): một tiến trình khi bị lỗi sẽ không thể phục hồi; đồng thời không tiếp tục gửi thông tin ra hệ thống.
• Thuật toán phải chạy đúng và kết thúc trên mọi cấu hình ban đầu.
• Thuật toán phải chạy đúng và kết thúc trong mọi trường hợp có thể thực thi.

Ta thấy FLP-Impossibility có rất nhiều ràng buộc mạnh, mà một số không khả thi trong thực tế (ví dụ như mạng bất đồng bộ). Do vậy, FLP-Impossibility không phải là “dấu chấm hết” trên con đường tìm kiếm thuật toán đồng thuận trong hệ thống phân tán.

Từ sau định lí FLP-Impossibility được phát biểu, các nghiên cứu bắt đầu tập trung làm rõ mô hình phù hợp với điều kiện thực tế, từ đó đưa ra thuật toán đồng thuận thỏa mãn mô hình đó. Một số hướng đi có thể để phát triển thuật toán đồng thuận:

• Thay đổi mô hình ban đầu: thay vì giả thiết là mạng bất đồng bộ, ta có thể chuyển thành mạng đồng bộ.
• Nới lỏng yêu cầu đầu ra thuật toán: thay vì toàn bộ các máy trong mạng cần đồng thuận trên cùng một giá trị, ta có thể đổi thành chỉ cần quá bán các máy đồng thuận. Hoặc ta chấp nhận một khả năng rất nhỏ thuật toán sẽ không thể kết thúc.
• Giảm nhẹ một số yêu cầu và đồng thời tăng mạnh một số yêu cầu khác. Ví dụ với hệ thống mạng đồng bộ (giảm yêu cầu về mạng) kết hợp với mô hình lỗi là Byzantine (tăng yêu cầu về mô hình chịu lỗi), ta chứng minh được có thể đạt được đồng thuận khi số máy tính lỗi không quá 1/3.

Minh họa một số mô hình lỗi

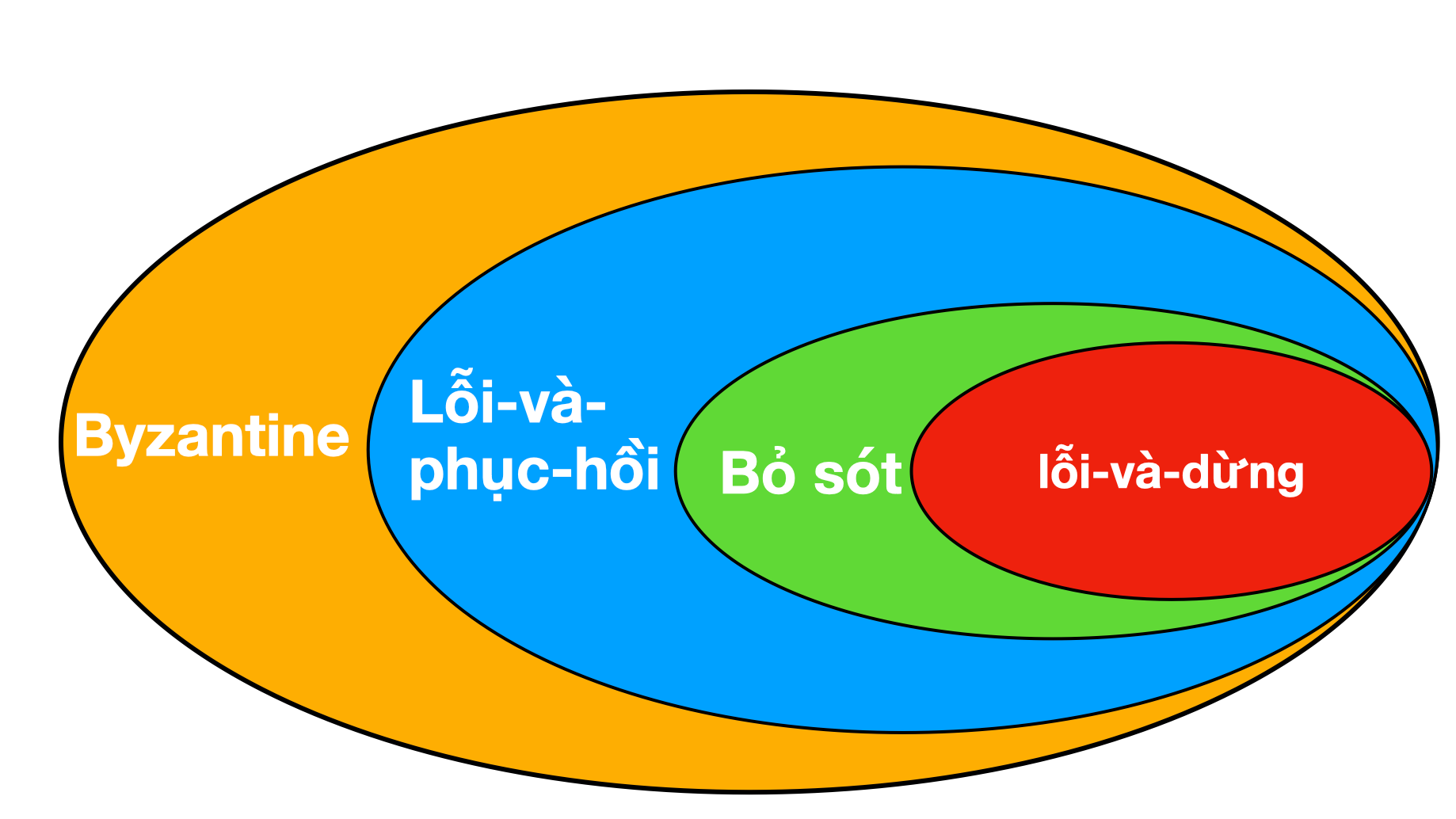
Ta có thể tóm lược lại một số mốc thời gian quan trọng như sau:

• Năm 1989, Lesie Lamport đưa ra báo cáo đầu tiên về thuật toán Paxos, tuy nhiên không nhiều nhà khoa học hiểu được.
• Năm 2001, Lesie Lamport viết lại paper Paxos với cách trình bày dễ hiểu hơn. Tuy nhiên, cách tiếp cận vẫn mang nhiều tính lí thuyết. Các hiện thực dựa trên Paxos sau này do vậy đều có những điểm khác nhau.
• Đến năm 2013, báo cáo đầu tiên thuật toán Raft ra đời. Theo như nghiên cứu, Raft đơn giản và phù hợp để học hơn Paxos cho những người mới tìm hiểu về thuật toán đồng thuận. Do vậy, Raft là đối tượng nghiên cứu chính của bài viết này.

Trong phần tiếp theo, chúng ta sẽ đi qua chi tiết về thuật toán Raft.