Bài viết sẽ giới thiệu các biến thể của Paxos, nhằm mục đích tâng performance, high-availability cho thuật toán.

Flexible Paxos

Paper Flexible Paxos: Quorum intersection revisited

Ý tưởng

Trong các bài toán về đồng thuận, việc sử dụng thuộc tính quá bán (tổng số node > N/2) cho quorum là rất quan trọng: khi đó 2 quorum bất kì đều sẽ giao ít nhất là một node. Ví dụ thực tế là ZooKeeper; etcd cluster với 3 và 5 nodes sẽ đạt được đồng thuận nếu có ít nhất lần lượt 2 và 3 nodes hoạt động tốt. Một đặc điểm quan trọng khi sử dụng quá bán cho quorum: giao giữa 2 quorum bất kì luôn có tối thiểu một node chung.

Điểm qua cách chứng minh của Paxos / Multi-Paxos / Raft đều tận dụng tính chất quan trọng trên: giao giữa 2 phase Prepare và Propose (Paxos) hoặc leader election và log replication (Raft) đều phải giao nhau bởi ít nhất một node.

Tuy nhiên, ta nhận thấy một điểm quan trọng: thuật toán nói chung, hay cách chứng minh nói riêng, sử dụng thuộc tính giao giữa 2 quorum của 2 phase khác nhau (Raft: Leader election và Log Replication, Single-decree Paxos: Prepare và Propose phase) luôn giao tối thiểu một node. Hay nói cách khác, không có điều kiện ràng buộc về giao giữa 2 quorum bất kì trong cùng một phase. Do vậy, ta thấy việc sử dụng quá bán cho quorum là chặt hơn mức cần thiết.

Paper về “Flexible Paxos” mở rộng khái niệm trên: nếu ta vẫn cố gắng để 2 phase giao nhau bởi tối thiểu một node, nhưng kích thước ở mỗi phase khác nhau, thì đồng thuận vẫn được đảm bảo. Cụ thể:

  • X là số node đồng ý gói tin Prepare(N)
  • Y là số node đồng ý gói tin Propose(N, V)

Nếu X + Y > N, với N là tổng số node trong hệ thống, thì đồng thuận vẫn đảm bảo.

Nhận xét này là cực kì hiệu quả trong vận hành. Cụ thể là khi Paxos mở rộng qua mô hình single leader, gói tin Prepare(N) đóng vai trò như leader election, Propose(N, V) đóng vai trò như log replication khi người dùng gửi request. Khi đó, số gói tin Prepare(N) nhỏ hơn rất nhiều với số gói tin Propose(N, V). Do vậy ta có thể tăng số node đồng thuận ở phase 1 và giảm số node đồng thuận ở phase 2 để giảm lưu lượng các gói tin gửi trong hệ thống.

Ví dụ với hệ thống có 10 node: số node đồng ý phase Prepare(N) tối thiểu là 8; số node đồng ý phase Propose(N, V) tối thiểu là 3 thì hệ thống vẫn an toàn và đạt được đồng thuận.

Đây là ví dụ minh họa trường hợp trên:

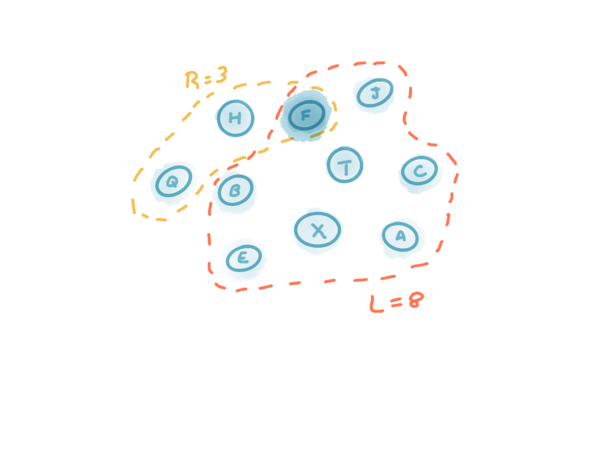
quorum

Ý tưởng này rất giống với Cassandra. Gọi R là số node đồng ý việc read và W là só node đồng ý việc ghi. nếu R+W > N thì hệ thống đạt được high consistency. từ đó engineer có thể tinh chỉnh 2 tham số R và W tùy thuộc vào nhu cầu và đặc tính hệ thống.

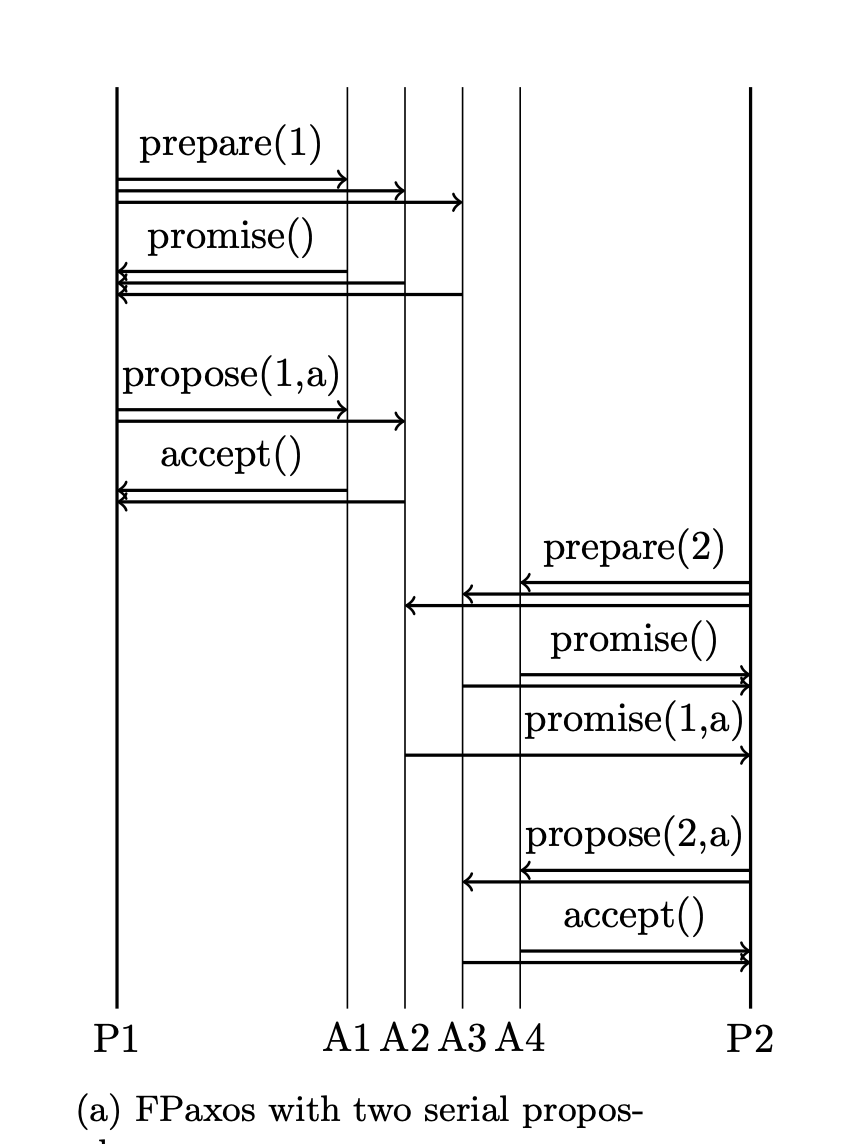Serial Hình minh họa với 2 serial proposals, với phase 1 (prepare), N = 3, và phase 2 (propose), M = 2. Ta dễ dàng thấy proposal thứ 2 có thể learning từ proposal thứ nhất thông qua common node giữa propose(1, a) và prepare(2)

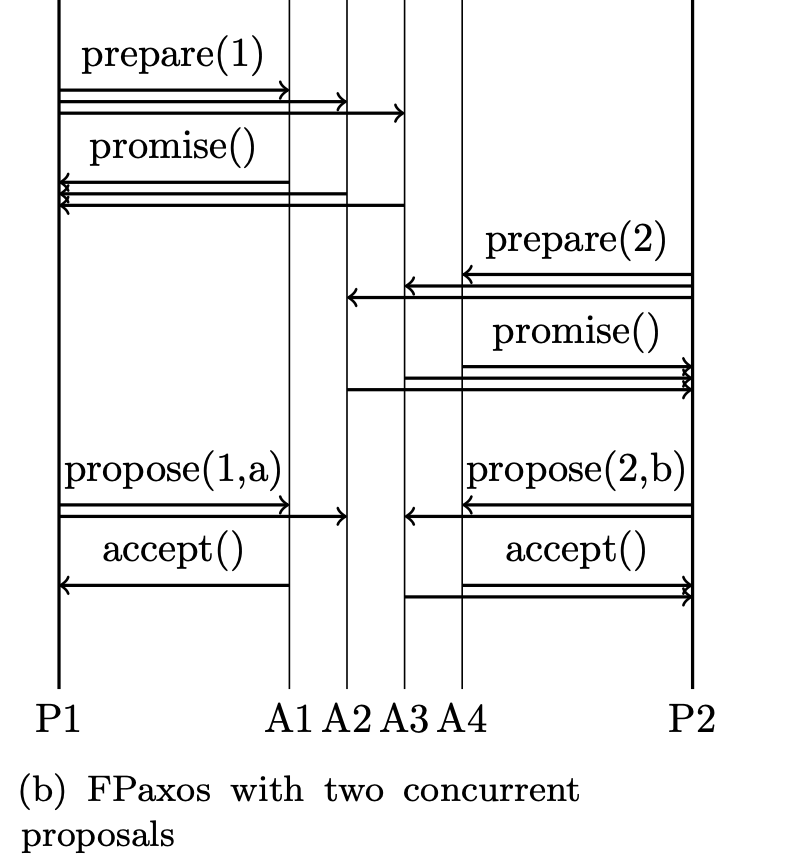Concurrent Hình minh họa với 2 proposal chạy song song. Ta thấy propose(1, a) sẽ luôn learn được từ prepare(2) thông qua một common node là A2.

Kết quả

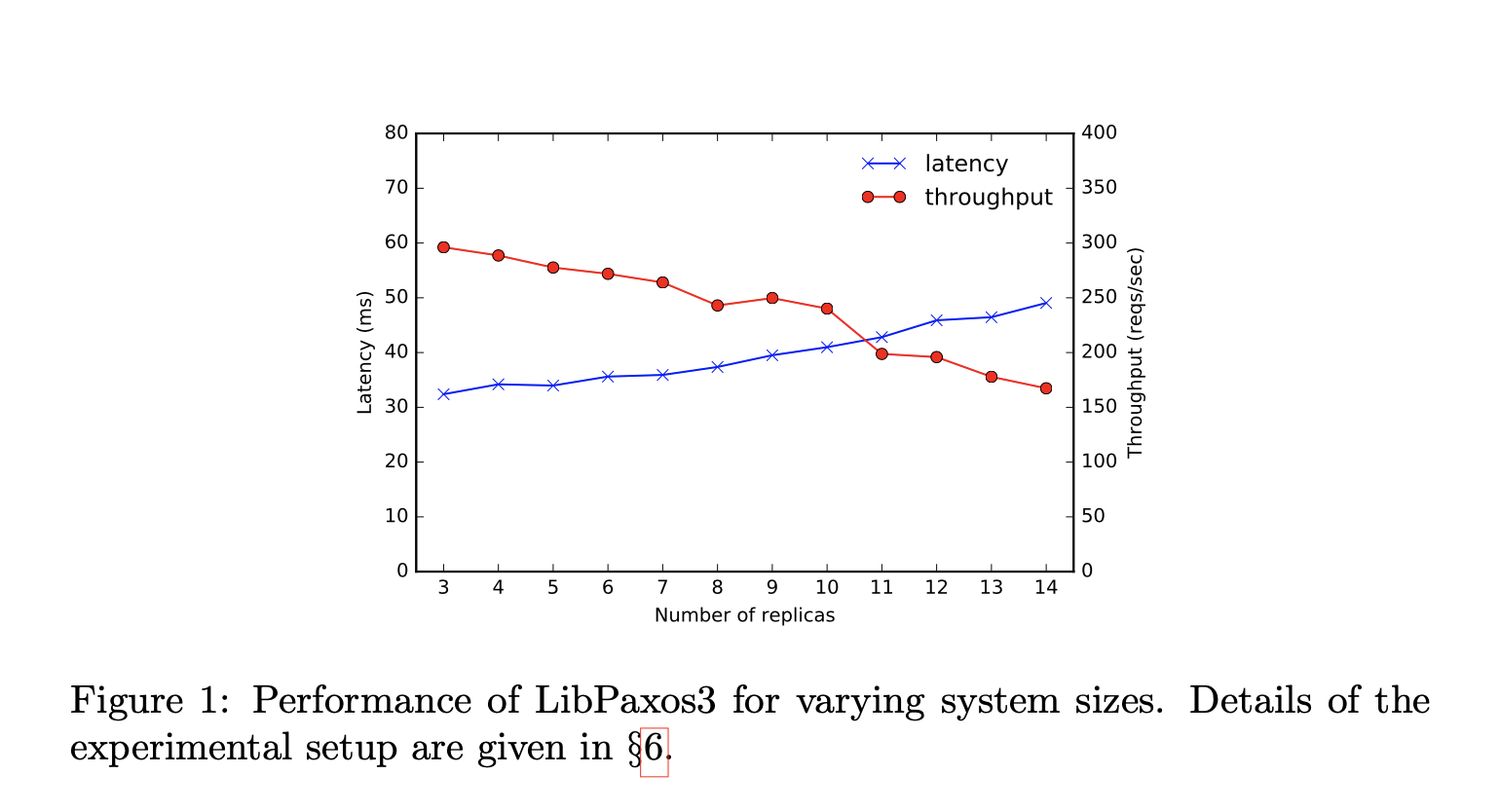
Vanila

Với Paxos bình thường, khi số replica tăng lên, thì throughput sẽ giảm và đồng thời latency sẽ tăng.

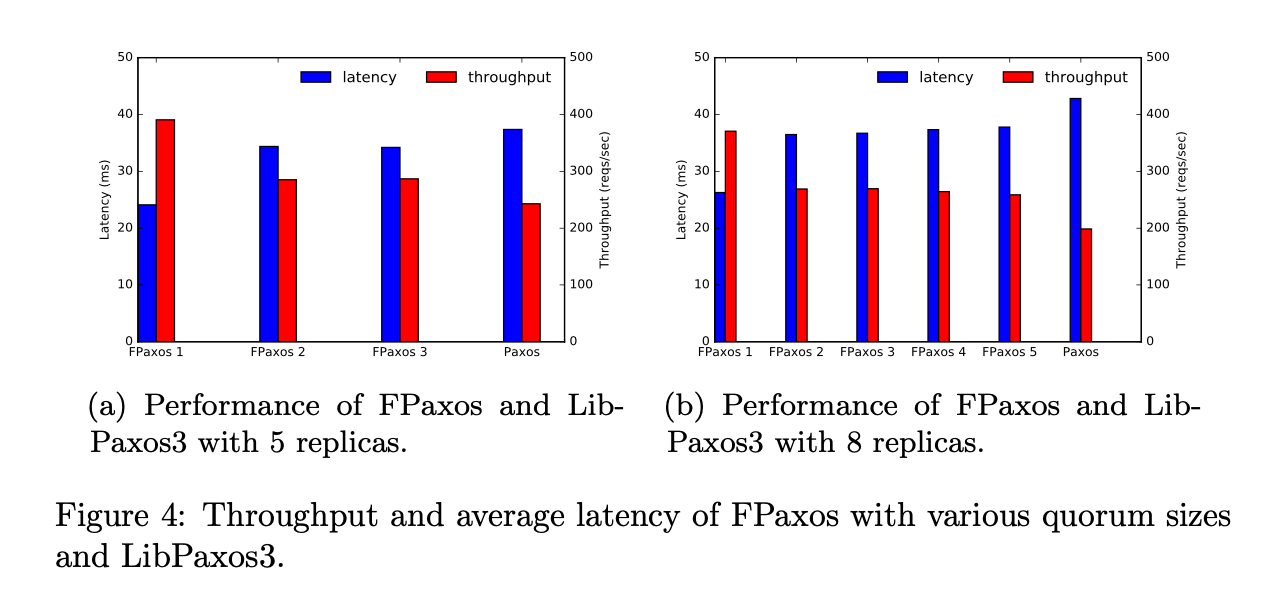
FPaxos Benchmark

Kết quả cho thấy Fast Paxos khi số replicas giảm dần ở phase 2 thì latency giảm và throughput tăng, và luôn có hiệu năng cao hơn vanilla Paxos.

Nhận xét về paper

Điểm mạnh

  • Là một phát biểu rất mạnh, có thể cải thiện việc thực thi Paxos trong hệ thống phân tán
  • Kết quả này rất là flexible, và có thể áp dụng cho các thuật toán đồng thuận khác như Raft - TLA Proof
  • Có đầy đủ chứng minh

Điểm yếu:

  • Không rõ có thể kết hợp optimisation này với các optimisation khác vốn có trên Paxos hay không (ví dụ: Fast Paxos)

Chứng minh

Định lí

Nếu giá trị v được decide với proposal p, thì với bất kì bộ proposal (p’, v’) nào mà p’ > p, v’ = v.

Nói cách khác, đồng thuận sẽ đạt được tối đa trên một giá trị.

Chứng minh

Ta sẽ chứng minh phản chứng. Giả sử tồn tại một proposal (p’, v’) mà p’ > p và v’ != v. Không mất tính tổng quát, giả sử p’ là giá trị nhỏ nhất thỏa mãn yêu cầu trên. (*)

Gọi S1 và S2 lần lượt là tập hợp các node có thể xảy ra ở phase 1 và phase 2, và A là tập hợp các acceptor trong hệ thống.

Ta có nhận xét:

  • ∀Q1 ∈S1 :Q1 ⊆A
  • ∀Q2 ∈S2 :Q2 ⊆A
  • ∀Q1 ∈S1, ∀Q2 ∈S2 :Q1 ∩Q2 != ∅ (1)

Lí do: theo cách xây dựng của Flexible Paxos, giao của 2 quorum bất kì ở phase 1 và phase 2 luôn giao tối thiểu tại một node. (Điều nay không đảm bảo cho 2 quorum trên cùng phase - như Paxos).

  • Gọi Q2,p là phase 2 quorum với proposal number p
  • Gọi Q1,p’ là phase 1 quorum với proposal number p’

Theo như (1), Q2,p và Q1,p’ giao nhau ít nhất tại một acceptor, ta gọi là A.

→ Tại sao ta chọn giữa 2 group là (Q2,p và Q1,p’) mà không phải ngược lại (Q2,p’ và Q1,p)?

→ Lí do: ta muốn chứng minh trường hợp: khi hệ thống đang run ở epoch trước (epoch = p), sau đó xảy ra sự kiện leader election (epoch = p’), hệ thống tiếp tục đạt được đồng thuận.

Tham khảo lại thuật toán Paxos, với một proposal X (p, m):

Phase 1:

  • Request: Proposer — prepare(p) —> Acceptor
  • Response: Acceptor — promise() —> Proposer

Phase 2:

  • Request: Proposer — propose(p, v) —> Acceptor
  • Response: Acceptor — accept() —> Proposer

Với quorum Q1,p’, ta lấy request prepare(p’). Với quorum Q2,p, ta lấy request propose(p, v). Xét thứ tự prepare(p’) và propose(p, v) nhận được trên acceptor A nêu trên:

Trường hợp 1: Acceptor A nhận prepare(p’) trước propose(p, v)

Do p’ > p, do vậy acceptor khi nhận được propose(p, v) sẽ reject. Vô lí, vì acceptor A theo giả thuyết sẽ đồng ý request propose(p, v)

Trường hợp 2: Acceptor A nhận được prepare(p’) sau propose(p, v)

Trường hợp 2A: proposal number mà Acceptor A nhận được lớn hơn p’ → Acceptor A sẽ reject prepare(p’) → vô lí theo giả thuyết.

Trường hợp 2B: proposal number mà Acceptor A nhận được nhỏ hơn p’ → Acceptor A sẽ đồng ý gói tin prepare(p’), đồng thời trả về gói tin Promise(q, v), với p <= q < p’ (2)

  • q >= p: vì acceptor sẽ gửi về epoch lớn nhất từng được observe, mà acceptor A đã từng observe được p, do vậy q >= p
  • value là V: theo trường hợp 2, acceptor A đã accept propose(p, v) trước đó, do vậy sẽ luôn trả về v - theo thuật toán Single-decree Paxos

Theo thuật toán, Proposal P sẽ nhận được các gói tin Promise(q’, v’’) và tổng hợp lại. Xét một range [q, p’] - lưu ý: q < p’ do (2). Ta sẽ có 3 trường hợp:

  • Trường hợp 1: q’ < q: Promise(q, v) sẽ được chọn → giá trị là v
  • Trường hợp 2: q < q’ < p’: acceptor A’ trả về promise(q’, v’’) thì (q’, v’’) trước hết phải được propose. Nếu v’’ != v, vi phạm việc (p’, v’) là proposal nhỏ nhất mà giá trị khác v - giả thuyết (*) phản chứng ban đầu. do vậy v’’ phải bằng v.
  • Trường hợp 3: p’ < q: Không xảy ra, vì acceptor chỉ reply với request prepare(p’) khi mà last promise < p’.

Từ 3 trường hợp trên, ta thấy: các promise(q’, v’’) bất kì trả về, hoặc là v, hoặc là sẽ bị từ chối. Do vậy, Proposer P sẽ lấy v. Điều này vô lí với giả thiết phản chứng: v’ != v → dpcm.