Bài viết sẽ chứng minh lại 3 định lí quan trọng trong thuật toán Raft: Log Matching Property; Leader Completeness và State Machine Safety Property.

Lí do

  • Implementation dựa vào figure 2 trong paper. Tuy nhiên, có vài chỗ không rõ nghĩa.
  • Nhiều đặc tả thuần về ngôn ngữ tự nhiên, cần có sự linh động khi implement. Tuy nhiên, linh động thế nào để việc thuật toán chạy vẫn chính xác ? –> Việc hiểu thuật toán là cần thiết.

Các định lí trong Raft

Định lí 1: Log Matching Property

Phát biểu (5.4.3)

- Statement 1: If two entries in different logs have the same index and term, then they store the same command.
- Statement 2: If two entries in different logs have the same index and term, then the logs are identical in all preceding entries.

Giải thích

Nếu 2 logs có ở một index bất kì có chung term, thì toàn bộ những entry trước đó ở cả 2 log đều tương đồng nhau (data + term + index)

Định lí này dùng để làm gì ? Được apply ở định lí tiếp theo, nếu ta tìm được ít nhất một message mà chung index và term ở 2 log L1 và L2, nếu log ở L1 trước đó có một message M → log ở L2 cũng phải có một message M.

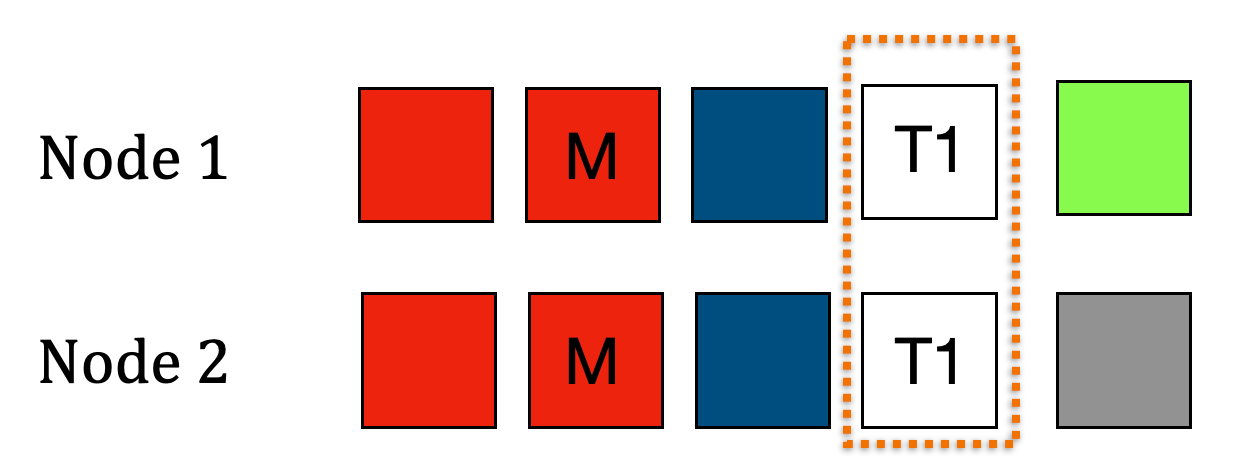
Chứng minh

Chứng minh ý 1

Ta thấy leader tạo tối đa một log entry tại một index và một term. Đồng thời, ta luôn duy trì thứ tự của một log entry ở mọi node (thông qua cơ chế Log Replication).

Ví dụ như log entry ở vị trí thứ 5 của node 1, khi được replicate qua node 2, ta phải đảm bảo log entry đấy cũng được duy trì ở vị trí 5. Do vậy, nếu 2 log có chung index và chung term, chúng phải có chung data.

Chứng minh ý 2

Theo như thuật toán về Log Replication, khi leader L gửi request AppendEntries tới một node follower: leader sẽ kèm theo index và term của log ngay trước thời điểm leader và follower đồng bộ log với nhau.

Nếu follower kiểm tra và không thấy log tại index đó có chung term -> đã có sự bất đồng bộ giữa follower và leader –> follower reject request và xoá toàn bộ các log entry từ đấy trở về sau.

Ta có thể quan sát bằng các bước sau:

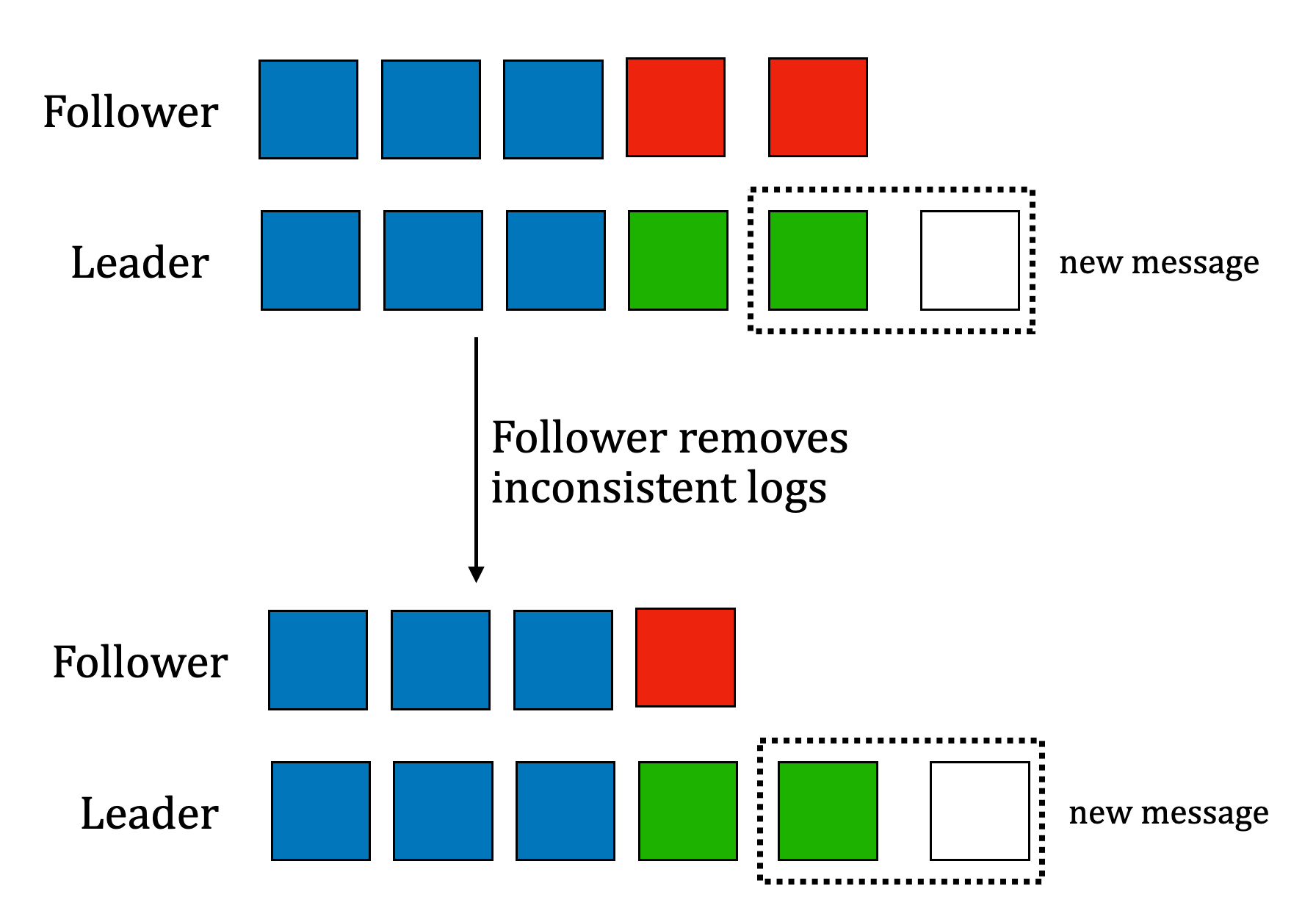Request AppendEntries 1: Remove first inconsistent logs

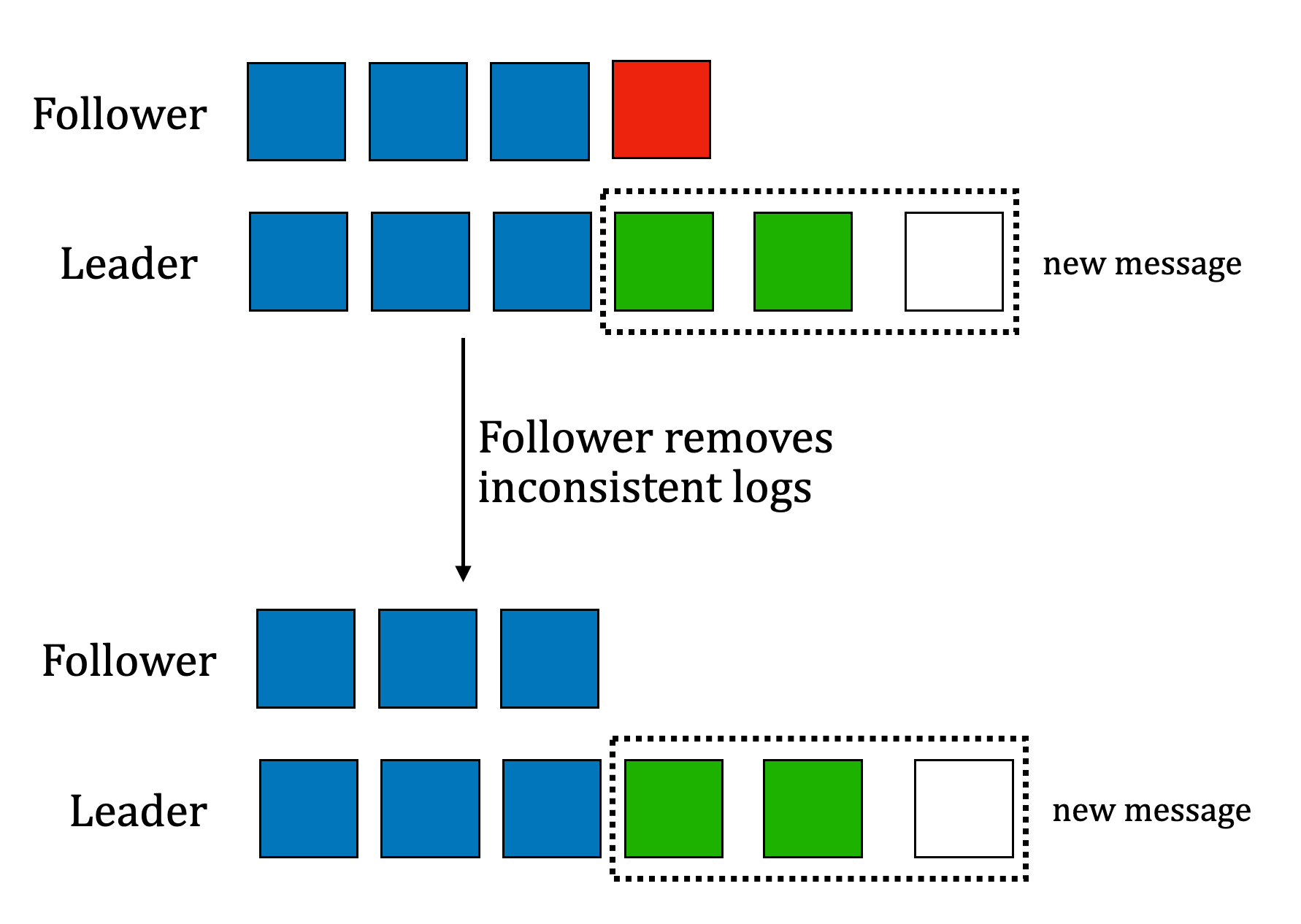Request AppendEntries 2: Remove second inconsistent logs

Request AppendEntries 3: Append all logs

Từ đó, ta có thể dễ dàng chứng minh định lí trên bằng quy nạp: với trường hợp khởi tạo, hiển nhiên đúng. Mỗi khi follower nhận được một request AppendEntries từ leader, follower sẽ kiểm tra và thường xuyên duy trì trạng thái consistent khi thêm vào một log.

Định lí 2: Leader completeness

Đây là định lí quan trọng nhất, và khó chứng minh nhất trong toàn bộ các định lí khác.

Phát biểu:

if a log entry is committed in a given term, then that entry will be present in the logs of the leaders for all higher-numbered terms.

Nếu một log entry đã được commit trong một term bất kì, thì log entry đó sẽ có mặt trong mọi log của mọi leader khác ở các term khác cao hơn.

Giải thích

  • Một log entry bao gồm 3 thuộc tính: data + term + index. Một log entry được commit sẽ được update vào FSM (Finate State Machine).
  • Định lí này đảm bảo trong mọi trường hợp, khi một log entry đã được update vào FSM ở thứ tự cho trước là K, thì ở bất kì leader nào khác (trong các term khác cao hơn), log entry đấy cũng sẽ được update ở thứ tự là K, với K = 1,2,3, … n (chứng minh ở định lí sau)
  • Nói cách khác, định lí đảm bảo các log entry sẽ được update lên FSM ở toàn bộ các node theo đúng một thứ tự duy nhất.

Chứng minh (dựa theo mục 5.4.3)

Trong bài chứng minh, sẽ có 9 ý. Tuy nhiên, ta có thể trình bày ngắn gọn hơn. Ta sẽ chứng minh định lí bằng phương pháp phản chứng.

Giả sử một leader ở term T1 commit một log entry M, nhưng log entry đó không được lưu trữ lại ở một leader nào đó ở term tương lai. Không mất tính tổng quát, giả sử term T2 là term nhỏ nhất (T2 > T1) mà leader tại term đó không có lưu trữ log entry đấy.

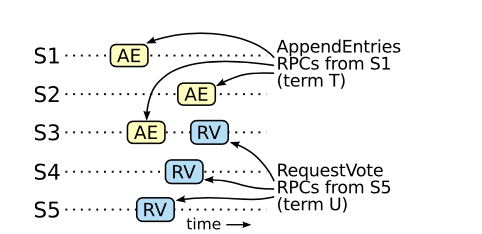
Giả sử như trong hình là một system có 5 node.

Chứng minh ý 1: Tồn tại một node S3 mà nhận được AppendEntries từ T1 và RequestVote từ T2 theo thứ tự tương ứng như hình vẽ trên

  • Vì log entry M đã được commit → phải có quá bán node trong hệ thống nhận được gói tin AppendEntries từ leader T1 về log entry M
  • Vì leader term T2 được bầu chọn → phải có quá bán node trong hệ thống nhận được gói tin RequestVote từ leader T2

→ Từ 2 ý trên, ta thấy phải tồn tại ít nhất một node mà đã accept gói tin AppendEntries và RequestVote từ leader T1 và T2 tương ứng, như trong hình là S3. Ở ý này, ta thấy mục đích của việc quá bán trong việc voting và gửi AppendEntries.

→ Gói tin AppendEntries phải đến trước gói tin RequestVote ở S3. Nếu ngược lại, S3 nhận được RequestVote (term T2) → AppendEntries (term T1), S3 sẽ reject gói tin AppendEntries vì T1 < T2 (vô lí).

→ Tồn tại một node S3 mà nhận được AppendEntries từ T1 và RequestVote từ T2 theo thứ tự tương ứng (dpcm)

Chứng minh ý 2:

Ta sẽ cố gắng loại đi một số trường hợp “râu ria” để có thêm nhiều dữ kiện mạnh cho chứng minh phần sau. Ở phần này ta sẽ tập trung khai thác dữ kiện Leader Restriction Rule.

S3 chấp nhận RequestVote cho leader term T2 → log ở leader term T2 khi đó more up-to-date hơn ở S3.

Ở bước chứng minh này, ta bắt đầu sử dụng dữ kiện leader restriction trong quá trình bầu chọn.

Section 5.4.1

[Condition 1] Raft determines which of two logs is more up-to-date by comparing the index and term of the last entries in the logs. If the logs have last entries with different terms, then the log with the later term is more up-to-date

[Condition 2] If the logs end with the same term, then whichever log is longer is more up-to-date.

Nói cách khác, một trong hai điều kiện sau phải thoả mãn:

  • Điều kiện 2: nếu log cuối cùng ở 2 node kết thúc ở cùng một term, node nào có log độ dài dài hơn là chiến thắng.

    • Do vậy, leader T2 phải có độ dài log >= độ dài log của node S3. Và theo phát biểu của định lí Log Matching, leader T2 phải có ít nhất toàn bộ log của S3 (có thể nhiều hơn). Vì S3 có chứa message M đã commit, do vậy leader T2 cũng phải chứa message M đã commit → mâu thuẫn với điều giả thiết phản chứng là leader T2 không chứa message M.

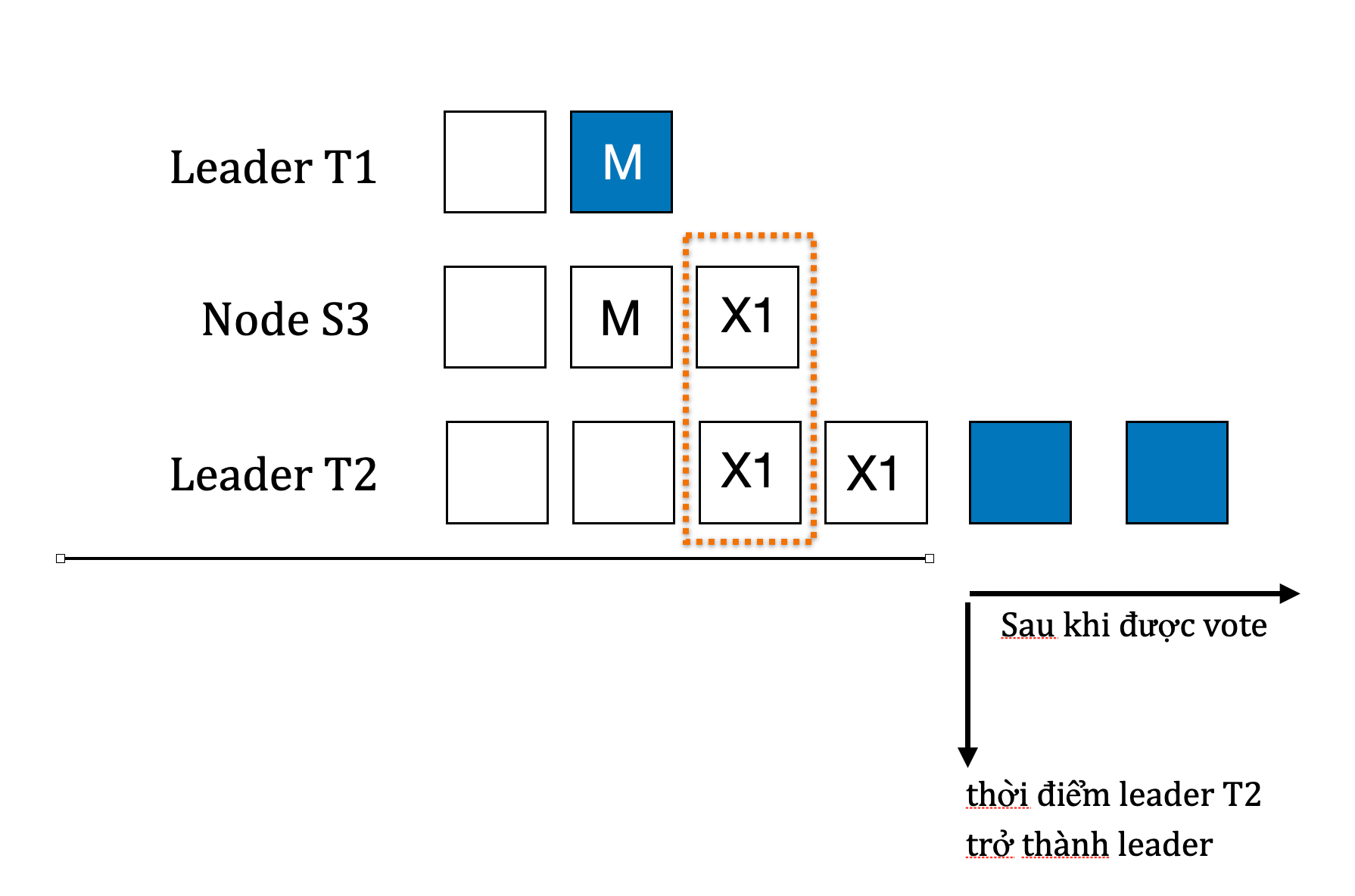
  • Điều kiện 1: log entry cuối cùng của leader T2 có term lớn hơn log entry cuối cùng của S3. Điều kiện này sẽ được sử dụng cho chứng minh ở ý sau.

Chứng minh ý 3:

  • Nhận xét 1: log entry cuối cùng của S3 ít nhất phải ở term T1 (vì S3 đã nhận AppendEntries từ leader T1). Theo như nhận xét ở chứng minh trên, last log entry của leader T2 lúc bầu chọn phải có term lớn hơn T1, tạm gọi là M2. (1)

  • Theo giả thuyết phản chứng, term T2 (T2 > T1) là term nhỏ nhất sau term T1 mà leader tại term đó không có lưu trữ log entry M. → như vậy, mọi leader trước T2 và sau T1 đều phải có message M. (2)

  • Leader T_1.5 là leader ngay trước Leader T2 mà tạo ra message M2. Theo như ý (1), M2 phải có term lớn hơn T1. Dựa theo hình vẽ trên, ta thấy:
    • Leader T_1.5 là leader ở term > T1 (nếu không sẽ không tạo ra được message M2 có term > T1)
    • Leader T_1.5 là leader ở term mà < T2 (do leader T2 được tạo sau leader T_1.5

→ theo như điều kiện (2), Leader T_1.5 phải chứa message M.

  • Theo định lí về Log Matching Property: Nếu 2 đoạn log tồn tại một entry cùng index và term, thì toàn bộ nội dung log từ đầu đến chính chỗ đấy tương tự nhau, thì leader tại vị trí T2 cũng phải tồn tại message M ngay thời điểm vote, mâu thuẫn.

–> Định lí được chứng minh

Định lí 3: State Machine Safety Property

Phát biểu

if a server has applied a log entry at a given index to its state machine, no other server will ever apply a different log entry for the same index.

Giải thích

Nếu một server đã apply một log entry vào State machine, không tồn tại server nào apply một log entry khác ở cùng một index.

Nói cách khác, ở một node bất kì:

  • Nếu node đó có term < T, node đấy sẽ chưa được apply log entry tại vị trí T
  • Nếu node đó có term >= T, tại vị trí T, node đấy sẽ apply cùng log entry giống với mọi server khác.

Chứng minh

Ta có thể chứng minh phản chứng như sau:

  • Giả sử tồn tại một follower mà có index tại K khác với bất kì một node nào có index tại K những đã commit lên FSM → leader truyền cho node mà index tại K cũng phải có giá trị khác.

  • Dựa vào định lí Leader Completeness, tất cả các leader của các term sau đó đều phải lưu trữ các log entry tương tự nhau → vô lí.

  • Do vậy, follower có index tại K phải chung giá trị với các node khác.

  • Do việc apply lên FSM diễn ra tuần tự theo index=0,1,2,… → dẫn đến định lí State Machine Safety Property